By Justin de Benedictis-Kessner
Experiments have undeniably increased in their use within political science in the last twenty years (Druckman et al., 2006). Especially frequent in this rise of experimental research is the survey experiment. Survey experiments are an effective method for exploiting random assignment to determine accurate causal effects while keeping the costs of research low and the speed with which data can be collected short (Mullinix et al., 2015). Moreover, survey experiments are a research methodology that can be accessible and open to many: students and faculty with varying degrees of resources can often use convenience samples to assess experimental treatment effects without great cost.
Yet while survey experiments, and in particular the use of convenience samples such as Amazon.com’s Mechanical Turk (MTurk), can make causal inference cheap and fast, sometimes the hurdles associated with designing and implementing the actual experiment can stymie researchers. Accomplishing basic randomization is not always easy within standard survey software platforms, and less basic randomization can be even more difficult (or impossible). In particular, complex randomization, such as assigning multiple options from a larger set of options — n choose p — and block randomization are not easy to implement using off-the-shelf survey software.
Moreover, standard survey practices such as presenting different information to respondents based on their answers earlier in a survey using a “lookup table” can be difficult to implement. Yet practices such as blocked randomization are standard in experimental research more broadly and can help researchers to improve statistical efficiency (e.g., Horiuchi, Imai, and Taniguchi, 2007; Imai, King, and Stuart, 2008; Moore, 2012). Ensuring access for all types of researchers conducting survey experiments to these experimental practices is therefore important for political science as a discipline more generally to produce better experimental results.
In this short post, I walk through several examples of how survey researchers can use Javascript to accomplish commonly needed survey tasks without advanced knowledge of the Javascript language. Much of this more complex functionality can be accomplished via Javascript embedded into the survey questions in Qualtrics, a common survey software platform. The Qualtrics platform is an industry-standard for running online public opinion, marketing, and experimental survey research. Researchers — in academia and elsewhere — rely on the platform to host their surveys usually because they are at institutions or companies that have site licenses, eliminating the cost for individual researchers to use the platform. The platform makes question layout and basic experimental designs easy to implement via a WYSIWYG user interface.
The first of these is simply randomization: picking one option out of many options, which can be time-consuming and difficult to implement using the built-in Qualtrics randomization functionality when the potential options are very numerous. This method can be extended to accomplish n choose p randomization – that is, choosing a set number of options from a larger set of many options — which is not possible via built-in Qualtrics randomization features. Third, I show how to accomplish block randomization among blocks created by respondent-entered characteristics. Finally, I demonstrate a technique useful for survey researchers in both experimental and non-experimental settings: using a lookup table to present certain information based on a unique identifier, respondents’ panel characteristics, or respondents’ answers.
Applications of Javascript in Qualtrics
Randomization by picking one option from many options
Basic randomization can easily be accomplished in Qualtrics via the “Survey Flow” tool of any survey project, which has a built-in “Randomizer” element that allows the researcher to assign p number of n choices to the respondent. Using embedded data elements, the researcher can then assign a respondent to one of n treatment groups randomly. If the research would like complete randomization (e.g. in cases of smaller sample sizes), they should check the “evenly present elements” option (Figure 1).
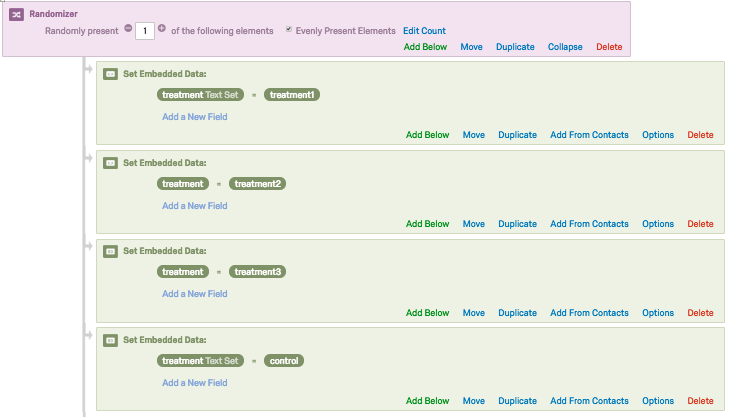Figure 1: Basic Randomization via Survey Flow
This is a simple and easily-implemented solution for the researcher, yet it be- comes much more difficult as the number of experimental treatments (n) increases. For instance, a researcher might want to present many different campaign ads to respondents, or vary a treatment along multiple dimensions. In this world of larger n treatments options, using the built-in survey flow randomizer to add options be- comes tedious and prone to human error. In contrast, this sample functionality can be easily accomplished by embedding Javascript in the question text of the survey prior to when the experimental treatments are to appear. Simply put, this allows the user to paste a longer list of n treatment options into a Javascript array which is then randomly shuffled, and then one p option chosen and assigned as the treatment condition. To accomplish randomization this method uses what is called a Fisher-Yates shuffle. The Javascript code for this simple randomization is below, and is also available publicly on GitHub: “Randomize QT pickone.js.”
Qualtrics.SurveyEngine.addOnload(function(){
function shuffle(array){
var counter = array.length,
temp, index;
while (counter > 0){
index = Math.floor(Math.random() * counter);
counter = counter-1;
temp = array[counter];
array[counter] = array[index];
array[index] = temp;
}
return array;
}
var myArray=["treatment1", "treatment2", "treatment3",
"treatment4", "treatment5", "treatment6", "treatment7",
"treatment8", "treatment9", "treatment10", "treatment11",
"treatment12", "treatment13", "treatment14", "control"];
shuffle(myArray);
Qualtrics.SurveyEngine.setEmbeddedData("treatment",myArray[0]);
});
Randomization by picking more than one option from many options
Sometimes, a researcher might wish to randomize each respondent into more than one condition — for instance, when having respondents view multiple articles to ascertain the effects of media on political preferences. In this case, the researcher would want to use an n choose p technique to assign possible options to a respondent. The Javascript used in the first example above can be easily adapted to serve this purpose. In this instance, I use the hypothetical example of a researcher wishing to assign a respondent five media articles from a list of fifteen. The Javascript code for this is below, and is also available on GitHub: “Randomize QT pickmany.js.”
Qualtrics.SurveyEngine.addOnload(function(){
function shuffle(array){
var counter = array.length,
temp, index;
while (counter > 0){
index = Math.floor(Math.random() * counter);
counter = counter-1;
temp = array[counter];
array[counter] = array[index];
array[index] = temp;
}
return array;
}
var myArray=["treatment1", "treatment2", "treatment3",
"treatment4", "treatment5", "treatment6", "treatment7",
"treatment8", "treatment9", "treatment10", "treatment11",
"treatment12", "treatment13", "treatment14", "treatment15"];
shuffle(myArray);
Qualtrics.SurveyEngine.setEmbeddedData("first_article",myArray[0]);
Qualtrics.SurveyEngine.setEmbeddedData("second_article",myArray[1]);
Qualtrics.SurveyEngine.setEmbeddedData("third_article",myArray[2]);
Qualtrics.SurveyEngine.setEmbeddedData("fourth_article",myArray[3]);
Qualtrics.SurveyEngine.setEmbeddedData("fifth_article",myArray[4]);
});
Block Randomization
This Javascript can also be adapted and combined with a web-hosted Shiny app to accomplish block randomization, a useful practice for increasing statistical efficiency in experiments. For instance, a researcher might want to block-randomize a treatment condition within different categories of respondents — usually a characteristic that the researcher believes will induce variation in the outcome. To block-randomize within a respondent characteristic, the researcher simply needs to create a question measuring that characteristic, and then randomize within values of that characteristic. For a limited number of characteristics or a small number of experimental conditions, this is easily accomplished with built-in branching based on respondent characteristics and completely randomizing within branches using the Qualtrics Survey Flow.
However, for a large number of options or background characteristics, adding these elements to survey flow becomes tedious. Using a combination of Javascript and a Shiny app hosted (for free) on shinyapps.io, however, you can make this a little easier. This Javascript uses my Shiny app to randomize among a (user-entered) number of experimental conditions within a block and pull that randomization into the Javascript to assign treatments within different categories, balancing assignment across conditions.
The R code to set up this Shiny App is available on GitHub under shinyapp/app.R and can be forked for users who with to use their own url for randomization. For users hoping to use my Shiny app url to randomize in their own surveys, make sure to create a unique surveyid in the Javascript. Users may also need to reset the treatment assignment randomization after testing. To do so, simply use a web browser to go to the following url, replacing “[surveyid]” with your surveyid for which you want to reset randomization: https://jdbk.shinyapps.io/blockrandomize/ ?surveyid=[surveyid]&reset=1
In this case, I wanted to block randomize the treatment used in the first example here by respondents’ eye color, which I asked about on my Qualtrics survey (Q56). Javascript code that can be adapted for this purposed is below, and is also available on GitHub: “Randomize QT byblock.js.”
Qualtrics.SurveyEngine.addOnload(function(){
// replace the QID below with the ID of variable you want to block on:
var blockvar = "${q://QID56/ChoiceGroup/SelectedChoices}";
// replace with your name + a unique name for your survey:
var surveyid = "jdbk-sample_block_randomize";
// replace with number of experimental conditions to randomize among:
var nconditions = "15";
var myArray=["treatment1", "treatment2", "treatment3",
"treatment4", "treatment5", "treatment6", "treatment7",
"treatment8", "treatment9", "treatment10", "treatment11",
"treatment12", "treatment13", "treatment14", "control"];
let xmlHttp = new XMLHttpRequest();
// the url below hits customizable shiny app with arguments set above
xmlHttp.open(’GET’, ’https://jdbk.shinyapps.io/blockrandomize/?surveyid=’+
surveyid + ’&blockvalue=’ + blockvar + ’&nconditions=’ + nconditions, false);
xmlHttp.send(null);
condition_assigned = xmlHttp.responseText; // get condition from randomizer
Qualtrics.SurveyEngine.setEmbeddedData("treatment",myArray[condition_assigned]);
});
Lookup tables
Finally, researchers sometimes wish to look up information about respondents based on previous panel information (for instance, information that corresponds to an ID number). Or perhaps a researcher wanted to present certain information to respondents based on their location and saved information about their representatives in that location. Doing so would require the use of a lookup table — that is, a table with information that can be queried with a key. Doing this is common in data analysis but is a less common (though still useful) practice in survey research. It can, however, be easily implemented in Qualtrics using a custom Javascript function and a user-inputted set of vectors corresponding to the matched information. Sample code that accomplishes this is below and also on GitHub: “Lookup QT.js.”
Qualtrics.SurveyEngine.addOnload(function()
{
var ID_block_table = {
ID: [’1’, ’2’, ’3’, ’4’, ’5’],
block: [’a’, ’b’, ’c’, ’d’, ’e’]
};
function getLookupTableByID(mytable, IDfield, ID, returnfield) {
matchindex = null;
try {
var matchindex = mytable[IDfield].indexOf(ID);
var matchreturn = mytable[returnfield][matchindex];
} catch (ex) {
console.log(ex);
}
return matchreturn;
}
var MID = Qualtrics.SurveyEngine.getEmbeddedData("MID");
var blockmatch = getLookupTableByID(ID_block_table, "ID", MID, "block");
Qualtrics.SurveyEngine.setEmbeddedData(’block’,blockmatch);
});
References
Druckman, James N, Donald P Green, James H Kuklinski, and Arthur Lupia. 2006. “The Growth and Development of Experimental Research in Political Science.” American Political Science Review 100(4): 627–635.
Horiuchi, Yusaku, Kosuke Imai, and Naoko Taniguchi. 2007. “Designing and Ana- lyzing Randomized Experiments: Application to a Japanese Election Survey Ex- periment.” American Journal of Political Science 51(3): 669–687.
Imai, Kosuke, Gary King, and Elizabeth A Stuart. 2008. “Misunderstandings Be- tween Experimentalists and Observationalists about Causal Inference.” Journal of the Royal Statistical Society: Series A 171(2): 481–502.
Moore, Ryan T. 2012. “Multivariate Continuous Blocking to Improve Political Sci- ence Experiments.” Political Analysis 20(4): 460–479.
Mullinix, Kevin J, Thomas J Leeper, James N Druckman, and Jeremy Freese. 2015. “The Generalizability of Survey Experiments.” Journal of Experimental Political Science 2(2): 109–138.